本文共 2994 字,大约阅读时间需要 9 分钟。
Tarjan(割点) - Electricity - POJ 2117
题意:
给定一个由 n 个点 m 条边构成的无向图,请你求出该图删除一个点之后,连通块最多有多少。
输入格式
输入包含多组数据。
每组数据第一行包含两个整数 n,m。
接下来 m 行,每行包含两个整数 a,b,表示 a,b 两点之间有边连接。
数据保证无重边。
点的编号从 0 到 n−1。
读入以一行 0 0 结束。
输出格式
每组数据输出一个结果,占一行,表示连通块的最大数量。
数据范围
1 ≤ n ≤ 10000 , 0 ≤ m ≤ 15000 , 0 ≤ a , b < n 1≤n≤10000, 0≤m≤15000, 0≤a,b<n 1≤n≤10000,0≤m≤15000,0≤a,b<n
输入样例:
3 30 10 22 14 20 12 33 11 00 0
输出样例:
122
分析:
目 标 即 在 所 有 连 通 分 量 中 选 择 一 个 割 点 , 使 得 删 除 该 点 后 分 出 的 连 通 块 数 量 最 多 。 目标即在所有连通分量中选择一个割点,使得删除该点后分出的连通块数量最多。 目标即在所有连通分量中选择一个割点,使得删除该点后分出的连通块数量最多。
如何判断割点:
条 件 : d f n [ u ] ≤ l o w [ j ] 。 条件:dfn[u]≤low[j]。 条件:dfn[u]≤low[j]。
① 、 若 u 不 是 根 节 点 , 删 除 u 以 后 , u 的 父 节 点 所 在 连 通 块 与 孩 子 节 点 所 在 连 通 块 将 分 成 多 个 部 分 。 此 时 u 是 割 点 。 ①、若u不是根节点,删除u以后,u的父节点所在连通块与孩子节点所在连通块将分成多个部分。此时u是割点。 ①、若u不是根节点,删除u以后,u的父节点所在连通块与孩子节点所在连通块将分成多个部分。此时u是割点。
情 况 ① 如 下 图 : 情况①如下图: 情况①如下图:
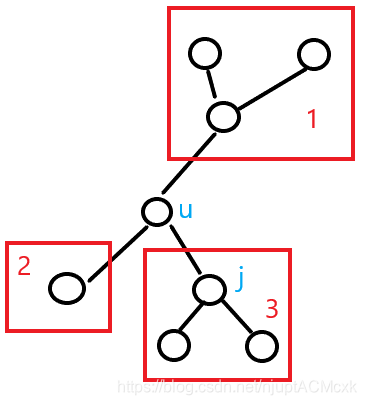 删 除 u 后 , 会 分 成 1 , 2 , 3 三 个 连 通 分 量 。 删除u后,会分成1,2,3三个连通分量。 删除u后,会分成1,2,3三个连通分量。
删 除 u 后 , 会 分 成 1 , 2 , 3 三 个 连 通 分 量 。 删除u后,会分成1,2,3三个连通分量。 删除u后,会分成1,2,3三个连通分量。 ② 、 若 u 是 根 节 点 , 那 么 u 至 少 有 两 个 孩 子 , 才 能 确 保 u 是 割 点 。 若 u 仅 有 一 个 孩 子 , 删 去 u 后 , 连 通 分 量 数 量 不 增 加 。 ②、若u是根节点,那么u至少有两个孩子,才能确保u是割点。若u仅有一个孩子,删去u后,连通分量数量不增加。 ②、若u是根节点,那么u至少有两个孩子,才能确保u是割点。若u仅有一个孩子,删去u后,连通分量数量不增加。
情 况 ② 如 下 图 : 情况②如下图: 情况②如下图:
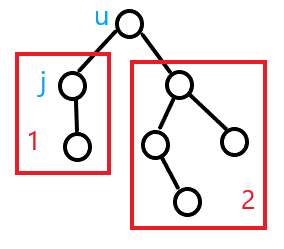
对条件的说明:
d f n [ u ] ≤ l o w [ j ] 。 dfn[u]≤low[j]。 dfn[u]≤low[j]。
等 号 是 可 以 取 的 。 取 等 时 u 与 j 或 j 的 孩 子 之 间 形 成 环 , 删 去 u 仍 然 会 与 j 分 开 。 等号是可以取的。取等时u与j或j的孩子之间形成环,删去u仍然会与j分开。 等号是可以取的。取等时u与j或j的孩子之间形成环,删去u仍然会与j分开。
d f n ] [ u ] > l o w [ j ] 时 , 即 u 在 环 的 内 部 , 删 去 u 就 不 能 够 增 加 连 通 分 量 的 数 量 。 dfn][u]>low[j]时,即u在环的内部,删去u就不能够增加连通分量的数量。 dfn][u]>low[j]时,即u在环的内部,删去u就不能够增加连通分量的数量。
具体步骤:
这 样 我 们 对 于 连 通 块 中 的 每 个 点 u , 统 计 满 足 d f n [ u ] ≤ l o w [ j ] 的 孩 子 j 的 数 量 。 这样我们对于连通块中的每个点u,统计满足dfn[u]≤low[j]的孩子j的数量。 这样我们对于连通块中的每个点u,统计满足dfn[u]≤low[j]的孩子j的数量。
有 一 个 j , 就 能 够 多 分 出 一 个 孩 子 连 通 分 量 。 有一个j,就能够多分出一个孩子连通分量。 有一个j,就能够多分出一个孩子连通分量。
注 意 , 若 u 不 是 根 节 点 , 最 后 还 需 要 增 加 一 个 父 节 点 所 在 的 连 通 分 量 。 注意,若u不是根节点,最后还需要增加一个父节点所在的连通分量。 注意,若u不是根节点,最后还需要增加一个父节点所在的连通分量。
用 全 局 变 量 a n s 来 更 新 去 除 每 个 点 能 够 分 出 的 连 通 块 数 量 的 最 大 值 。 用全局变量ans来更新去除每个点能够分出的连通块数量的最大值。 用全局变量ans来更新去除每个点能够分出的连通块数量的最大值。
记 连 通 块 总 数 初 始 为 c n t , 最 大 答 案 为 a n s + ( c n t − 1 ) 。 记连通块总数初始为cnt,最大答案为ans+(cnt-1)。 记连通块总数初始为cnt,最大答案为ans+(cnt−1)。
代码:
#include#include #include using namespace std;const int N=10010, M=30010;int n,m;int e[M],ne[M],h[N],idx;int dfn[N],low[N],timestamp;int root,ans;void add(int a,int b){ e[idx]=b,ne[idx]=h[a],h[a]=idx++;}void tarjan(int u){ dfn[u]=low[u]=++timestamp; int res=0; //统计割点能够将连通块分成几部分 for(int i=h[u];~i;i=ne[i]) { int j=e[i]; if(!dfn[j]) { tarjan(j); low[u]=min(low[u],low[j]); if(low[j]>=dfn[u]) res++; } else low[u]=min(low[u],dfn[j]); } if(u!=root) res++; ans=max(ans,res);}int main(){ while(~scanf("%d%d",&n,&m),n||m) { memset(h,-1,sizeof h); memset(dfn,0,sizeof dfn); idx=0,ans=0,timestamp=0; int a,b; for(int i=0;i
转载地址:http://jaor.baihongyu.com/